RN-《算法图解》

发表于 更新于 分类于

第一章 算法简介

二分查找

下面是二分查找的实现代码，// 代表向下取整。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def binary_search(list, item):
	low = 0
	high = len(list) - 1

	while low <= high:
		mid = (low + high) // 2
		guess = list[mid]
		if guess == item:
			return mid
		if guess > item:
			high = mid - 1
		else:
			low = mid + 1
	
	return None

my_list = [1, 3, 5, 7, 9]

print(binary_search(my_list, 3))  # 1

print(binary_search(my_list, -1))  # None

大 O 表示法

为检查长度为 n 的列表，二分查找需要执行 log n 次操作，使用大 O 表示法，可以表示为 O(log n)。

大 O 表示法指出了平均情况下的运行时间。

常见的大 O 表示法

O(log n)，也叫对数时间，如二分查找。

O(n)，也叫线性时间，如简单查找。

O(n * log n)，如快速排序。

O(n²)，如选择排序。

O(n!)，如旅行商问题。

启示

谈论算法的速度时，我们说的是随着输入的增加，其运行时间将以什么样的速度增加。

算法的运行时间用大 O 表示法表示。

第二章 选择排序

数组和链表

数组中的元素在内存中都是相连的，链表中的元素可存储在内存的任何地方。

比如六个人去看电影，数组就意味着六个一起的座位，链表相当于六个人分开坐。

链表的优势在插入元素方面，数组的优势在于随机读取元素。

数组 链表
读取 O(1) O(n)
插入 O(n) O(1)
删除 O(n) O(1)

选择排序

比如我想把自己听过的歌曲根据播放量从小到大排序，如果使用选择排序的话，就是先从全部的歌曲中找出播放量最少的写在纸上，然后找出第二少的再写到纸上，直到最后一个。

要找出播放量最少的歌曲，必须检查每一首歌，需要的时间是 O(n)，对于这种时间为 O(n) 的操作，需要执行 n 次。所以需要的总时间为 O(n * n)，即 O(n²)。

随着选择排序的进行，每一次需要检查的元素数在逐渐减少，到最后一次需要检查的元素只有一个，为什么运行时间还是 O(n n) 呢？这是因为从 n，n-1… 2，1，平均每次检查的元素数为 1/2 n，所以运行时间为 O(1/2 n n)，大 O 表示法省略了常数。

下面是选择排序的实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def findSmallest_index(arr):
	smallest = arr[0]
	smallest_index = 0
	for i in range(1, len(arr)):
		if arr[i] < smallest:
			smallest = arr[i]
			smallest_index = i
	return smallest_index

def selectionSort(arr):
    newArr = []
    length = len(arr)
    for i in range(length):
        smallest_index = findSmallest_index(arr)
        newArr.append(arr.pop(smallest_index))
    return newArr


print(selectionSort([5, 3, 6, 2, 10]))

第三章 递归

https://stackoverflow.com/questions/72209/recursion-or-iteration/72694#72694

Loops may achieve a performance gain for your program. Recursion may achieve a performance gain for your programmer. Choose which is more important in your situation!

第四章 快速排序

快速排序的原理：先从数组中选出一个基准值（pivot），然后找出比基准值大的元素和比基准值小的元素形成两个数组，然后合并成一个数组。

下面是快速排序的实现代码，进行了递归操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def quicksort(arr):
	if len(arr) < 2:
		return arr
	else:
		pivot = arr[0]
		less = []
		greater = []
		for i in range(1, len(arr)):
			if arr[i] <= pivot:
				less.append(arr[i])
			else:
				greater.append(arr[i])
		return quicksort(less) + [pivot] + quicksort(greater)

print(quicksort([10, 5, 2, 3]))

如果有 n 个元素，平均情况下可以分成 O(log n) 层，即栈长为 O(log n)，每层的运行时间为 O(n)，所以运行时间为 O(log n) O(n) = O(n log n)。

这一章的图画的挺好的

第五章 散列表

Python 提供的散列表实现为字典，可以使用 dict() 或者 {} 来创建散列表。

在访问 https://www.baidu.com/ 的时候，计算机将其转换为 IP 地址 180.76.76.76，这个过程被称为 DNS 解析，散列表是提供这种功能的方式之一。

散列表还可以用作网站的缓存：缓存是一种常见的加速方式，缓存的数据则存储在散列表中。

以下内容编程语言都实现好了

冲突

散列表可能出现冲突，处理冲突的办法有很多。

解决冲突最简单的办法：如果两个键映射到了同一个位置，就在这个位置存储一个链表。然而这就造成了性能的下降。

性能

良好的性能需要：较低的填装因子和良好的散列函数。

填装因子 = 散列表包含的元素数 / 位置总数，一旦填装因子超过0.7，就该调整散列表的长度。

散列函数最理想的情况就是将键均匀地映射到散列表的不同位置。

第六章 广度优先搜索

广度优先搜索（breadth-first search ，BFS）

相关的问题一般与队列有关，广度优先搜索一般能找出段数最少的路径。

下面是书中的一个实例，寻找名字中最后一个字母是 m 的人，一层一层朋友圈的寻找。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from collections import deque

def person_is_seller(name):
    return name[-1] == 'm'

graph = {}
graph["you"] = ["alice", "bob", "claire"]
graph["bob"] = ["anuj", "peggy"]
graph["alice"] = ["peggy"]
graph["claire"] = ["thom", "jonny"]
graph["anuj"] = []
graph["peggy"] = []
graph["thom"] = []
graph["jonny"] = []

def search(name):
    search_queue = deque()
    search_queue += graph[name]
    # This array is how you keep track of which people you've searched before.
    searched = []
    while search_queue:
        person = search_queue.popleft()
        # Only search this person if you haven't already searched them.
        if person not in searched:
            if person_is_seller(person):
                print(person + " is a mango seller!")
                return True
            else:
                search_queue += graph[person]
                # Marks this person as searched
                searched.append(person)
    return False

search("you")  # thom is a mango seller!

第七章 狄克斯特拉算法

  • 广度优先搜索用于在非加权图中查找最短路径。

  • 狄克斯特拉算法用于在加权图中查找最短路径。

  • 仅当权重为正时狄克斯特拉算法才管用。

实例

1

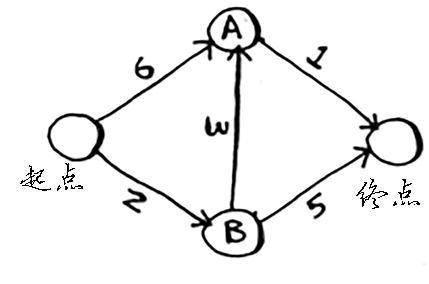
算法

2

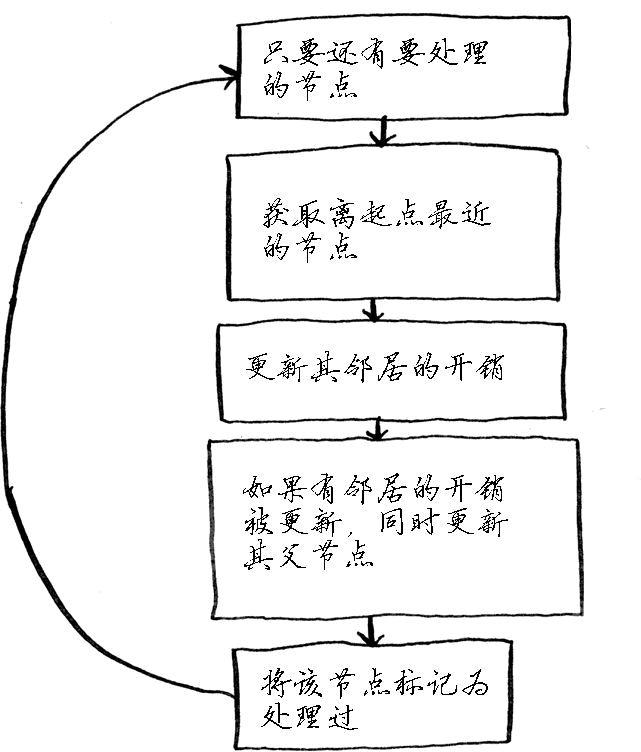
过程

首先遍历起点的邻居

父节点 节点 开销
起点 A 6
起点 B 2
终点 –

因为 B 的开销最小，更新 B 的邻居

父节点 节点 开销
B A 5
起点 B 2
B 终点 7

现在 A 的开销最小，更新 A 的邻居

父节点 节点 开销
B A 5
起点 B 2
A 终点 6

更新完成

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
# the graph
graph = {}
graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2

graph["a"] = {}
graph["a"]["fin"] = 1

graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["fin"] = 5

graph["fin"] = {}

# the costs table
infinity = float("inf")
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["fin"] = infinity

# the parents table
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = None

processed = []


def find_lowest_cost_node(costs):
    lowest_cost = float("inf")
    lowest_cost_node = None
    # Go through each node.
    for node in costs:
        cost = costs[node]
        # If it's the lowest cost so far and hasn't been processed yet...
        if cost < lowest_cost and node not in processed:
            # ... set it as the new lowest-cost node.
            lowest_cost = cost
            lowest_cost_node = node
    return lowest_cost_node


# Find the lowest-cost node that you haven't processed yet.
node = find_lowest_cost_node(costs)
# If you've processed all the nodes, this while loop is done.
while node is not None:
    cost = costs[node]
    # Go through all the neighbors of this node.
    neighbors = graph[node]
    for n in neighbors.keys():
        new_cost = cost + neighbors[n]
        # If it's cheaper to get to this neighbor by going through this node...
        if costs[n] > new_cost:
            # ... update the cost for this node.
            costs[n] = new_cost
            # This node becomes the new parent for this neighbor.
            parents[n] = node
    # Mark the node as processed.
    processed.append(node)
    # Find the next node to process, and loop.
    node = find_lowest_cost_node(costs)

print("Cost from the start to each node:")
print(costs)

第八章 贪婪算法

典型的问题：教室调度问题。不再作详细记录。

第九章 动态规划

每个动态规划问题都从一个网格开始，先解决子问题，在逐步解决大问题。这种问题就是找公式，画表格。

最典型的问题就是背包问题。

实例：背包最多装4斤东西，可选的东西有 3000 元的音响（4斤），2000 元的笔记本电脑（3斤），1500 元的吉他（1斤）。

这是计算公式。

4

这是根据公式画出的表格。

3

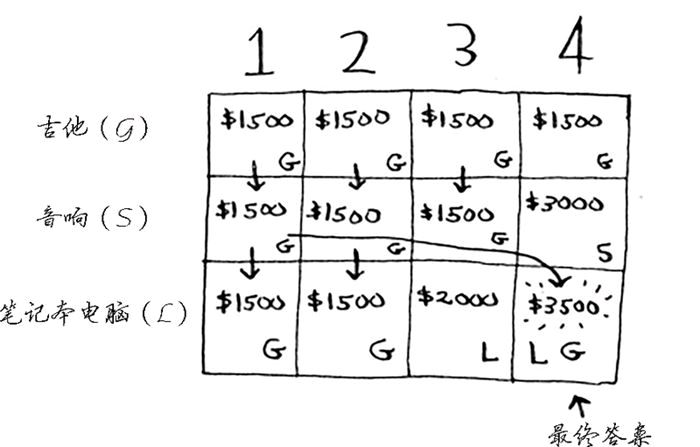
本书到此完结。